Tutorial 8 - Using A Custom Model Fit#
SAILS provides implementations of several algorithms for fitting autoregressive models but it is straightforward to create a custom class which implements a new model fit or uses one from another package.
This tutorial will outline how to create a custom model fit class using the
Vector Autoregression class from statsmodels.tsa. We start by importing SAILS
and creating a simulated time series to model.
import sails
# Create a simulated signal
sample_rate = 100
siggen = sails.Baccala2001_fig2()
X = siggen.generate_signal(sample_rate=sample_rate,num_samples=1000)
We then fit a model using Ordinary Least Squared as implemented in SAILS.
# Fit an autoregressive model with order 3
sails_model = sails.OLSLinearModel.fit_model(X, np.arange(4))
Before we continue, we should note that you can pass an existing sklearn
estimator (for example, sklearn.linear_model.LinearRegression as the
estimator parameter to the fit_model function of the OLSLinearModel
class. If you do this, you should not fit the intercept in the model. For
instance:
import sklearn.linear_model
# Fit an autoregressive model using SKLearn's LinearRegressor
estimator = sklearn.linear_model.LinearRegression(fit_intercept=False)
sails_model = sails.OLSLinearModel.fit_model(X, np.arange(4), estimator=estimator)
The above will give the same answers as the default method (which calculates the parameters using the normal equations). You can, however, extend this approach to use, for instance, ridge or lasso-regression using the relevant classes (sklearn.linear_model.Ridge or sklearn.linear_model.Lasso).
To go beyond what is available using the previous options, we can create a new
model fit class based on sails.modelfit.AbstractLinearModel. This is a base
class which contains a number of methods and properties to store and compute
information on a model. The AbstractLinearModel is not usable on its own
as the fit_model method is not implemented. When classes such as
OLSLinearModel are defined in SAILS, they inherit from
AbstractLinearModel to define the helper functions before a specific
fit_model method is defined. We can do the same to define a custom model
fit class using an external package. We will first create a new class which
inherits from AbstractLinearModel and then define a fit_model method
which computes the model fit and stores the outputs in a standard form.
Here is our custom model fit class, each section is described in the comments in the code.
# Define a new class inheriting from the SAILS base model
class TSALinearModel( sails.AbstractLinearModel ):
# Define a fit_model method using the python @classmethod decorator
@classmethod
def fit_model( cls, data, delay_vect):
# Some sanity checking of the input matrix We make sure that the input
# data is in 2d format or 3d format with a single epoch.
# statsmodels.tsa doesn't currently support fitting multitrial data
if data.ndim == 3:
if data.shape[2] > 1:
raise ValueError('This class is only implemented for single-trial data')
# Take first trial if we have 3d data
data = data[:,:,0]
# Create object - classmethods act as object constructors. cls points
# to TSALinearModel and ret is a specific instance of TSALinearModel
# though it is currently empty.
ret = cls()
# The rest of this method will populate ret with information based on
# our model fit
# Import the model fit function
from statsmodels.tsa.api import VAR
# Initialise and fit model - we use a simple VAR with default options.
# Note that we return the model and results to ret.tsa_model. This
# means that the statsmodels.tsa.api.VAR object will be stored and
# returned with ret. Later we can use this to access the statsmodels
# model and results though the SAILS object.
ret.tsa_model = VAR(data.T) # SAILS assumes channels first, TSA samples first
model_order = len(delay_vect) - 1 # delay_vect includes a leading zero
ret.tsa_results = ret.tsa_model.fit(model_order)
# The method must assign the following values for SAILS metrics to work properly
ret.maxorder = model_order
ret.delay_vect = np.arange(model_order)
ret.parameters = np.concatenate((-np.eye(data.shape[0])[:,:,None],
ret.tsa_results.coefs.transpose((1,2,0))), axis=2)
ret.data_cov = sails.find_cov(data.T,data.T)
ret.resid_cov = sails.find_cov(ret.tsa_results.resid.T,ret.tsa_results.resid.T)
# Return fitted model within an instance of a TSALinearModel
return ret
It is crucial that the fit_model class returns an instance of our the
overall class. This instance must contain the following information. Other
functions in SAILS assume that these are stored in a fitted model class with
specific formats and names.
maxorder: the model order of the fit
delay_vect: the vector of delays used in the model fit
parameters: the fitted autoregressive parameters of shape [num_channels x num_channels x model_order] with a leading identity
data_cov: the covariance matrix of the fitted data
resid_cov: the covariance matrix of the residuls of the fit
Other data can be added in as well (we store tsa_model and tsa_results
in the example here) but these five must be defined within the returned class.
We can now fit a model using our new class
tsa_model = TSALinearModel.fit_model(X,np.arange(4))
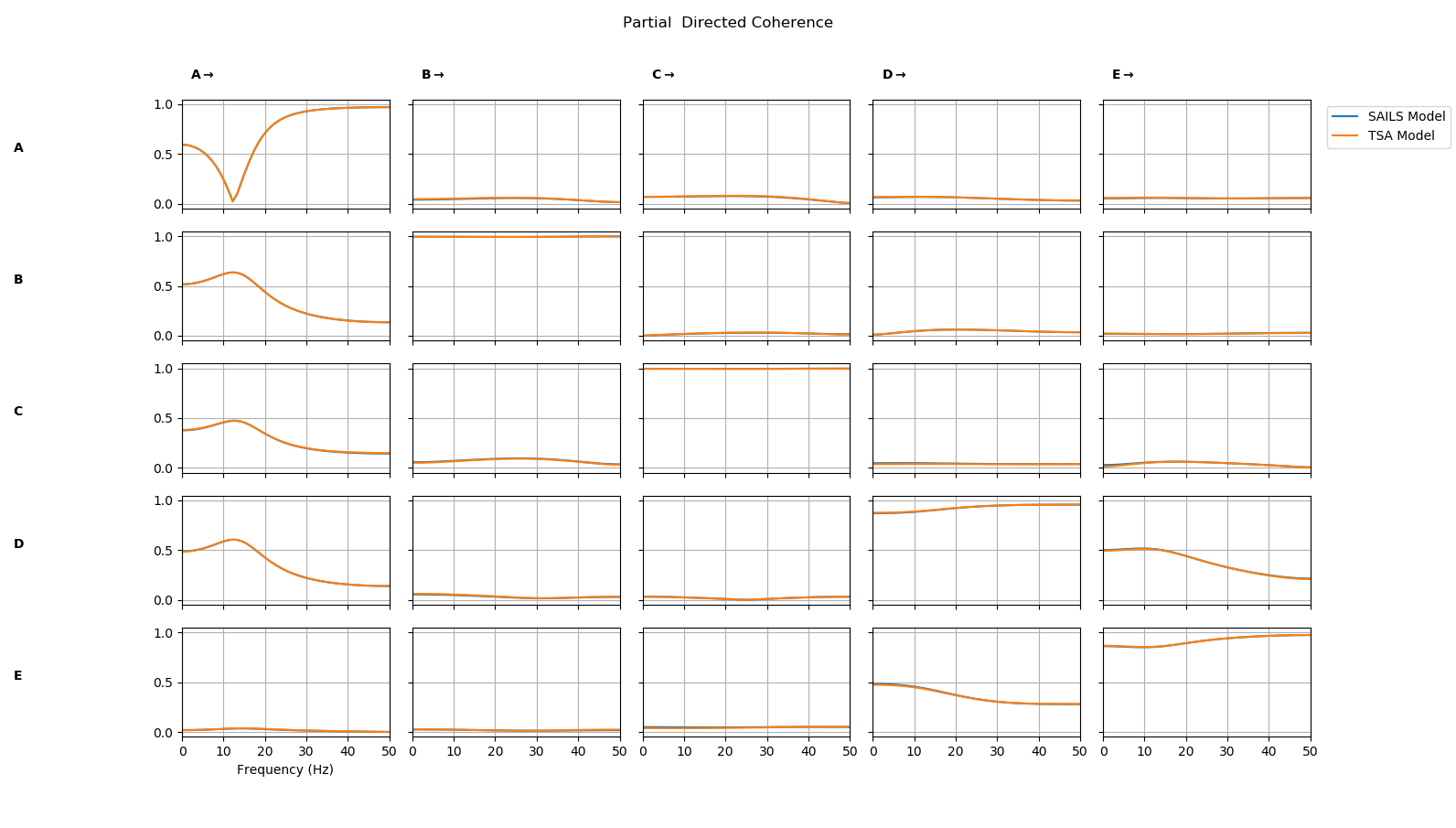
Finally, we compute connectivity metrics from each model fit and plot a comparison
freq_vect = np.linspace(0,sample_rate/2)
sails_metrics = sails.FourierMvarMetrics.initialise(sails_model,sample_rate,freq_vect)
tsa_metrics = sails.FourierMvarMetrics.initialise(tsa_model,sample_rate,freq_vect)
PDC = np.concatenate( (sails_metrics.partial_directed_coherence,tsa_metrics.partial_directed_coherence),axis=3)
sails.plotting.plot_vector(PDC,freq_vect,line_labels=['SAILS','TSA'],diag=True,x_label='Frequency (Hz'))
We see that the partial directed coherence from the two models is nearly identical.