Tutorial 5 - MVAR Connectivity Estimation#
In this tutorial, we will explore a range of connectivity estimators in a simulated network.
We start by importing sails and defining some meta-parameters as we did in previous tutorials.
import numpy as np
import sails
sample_rate = 128
We will use an example network from Baccala & Sameshima 2001. This is defined within the simulation module in Sails. We can import a signal generator based on figure 2 from Baccala & Sameshima 2001.
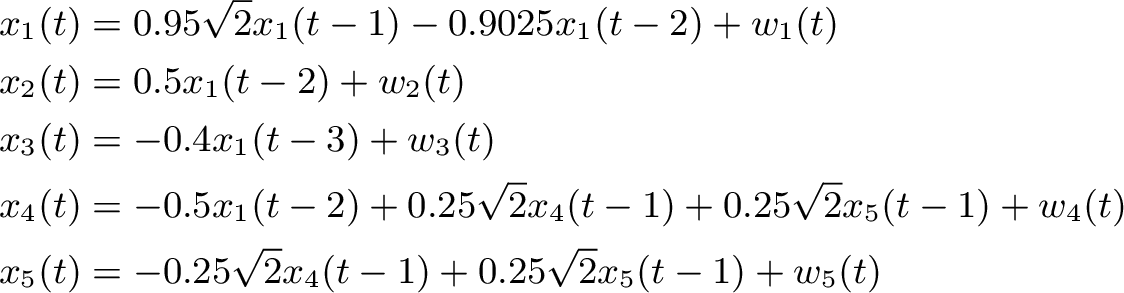
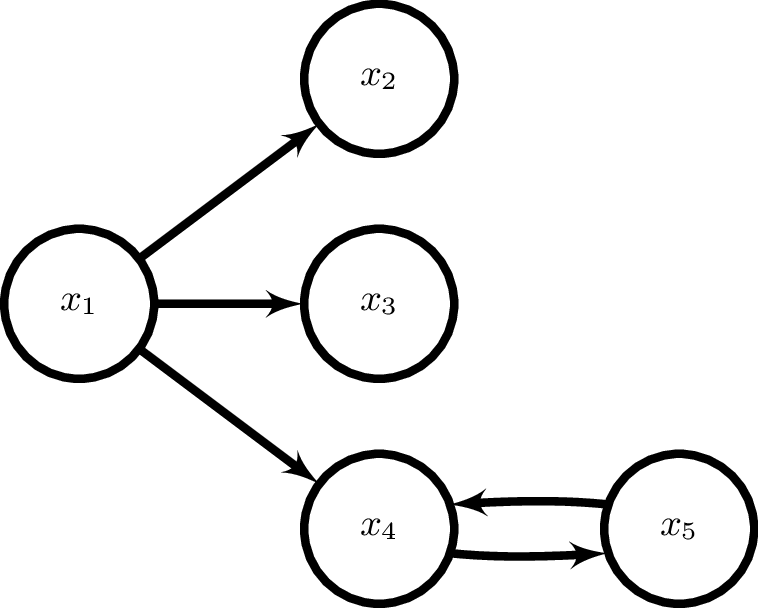
siggen = sails.simulate.Baccala2001_fig2()
The siggen object contains the autoregressive parameters defining the network and can create a model containing these parameters which we can use in further analyses. Here we create a model containing the ‘true’ autoregressive parameters and use it to compute the connectivity metrics.
m = siggen.generate_model()
freq_vect = np.linspace(0, sample_rate/2, 36)
F = sails.FourierMvarMetrics.initialise(m, sample_rate, freq_vect)
F is an object containing methods to compute a range of frequency domain connectivity metrics. Each metric is evaluated across the range of frequencies_defined in freq_vect and can be plotted using the plot_vector function in sails. Next we plot the Magnitude Squared Coherence estimated from our simulation parameter.
fig = sails.plotting.plot_vector(np.abs(F.S), freq_vect, diag=True)
fig.show()
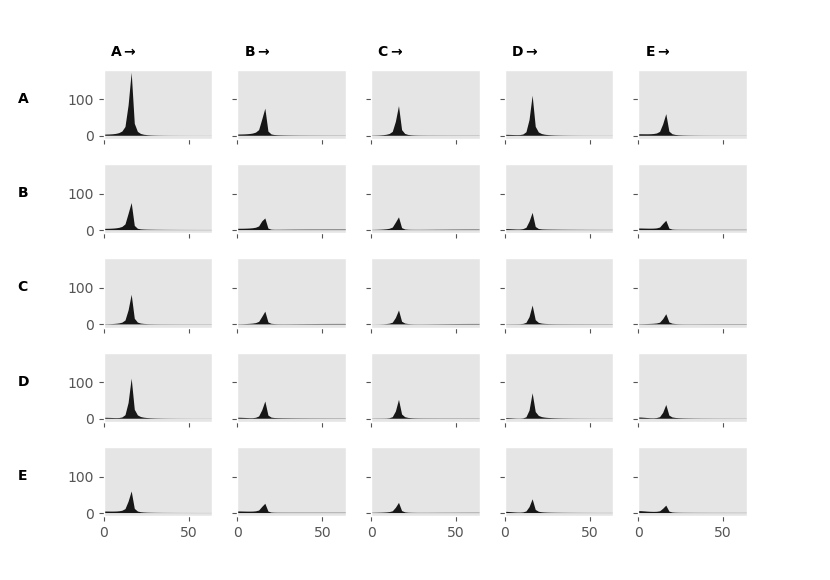
This will generate a matrix of plots, each plot represents the coherence as a function of frequency between the node specified in the column and row labels. In this case, we find that all our nodes are strongly coherence with each other. This is as the coherence does not distinguish between direct and indirect connections. For example, nodes 1 and 5 are only connected through node 4 yet the coherence still shows a connection. The coherence is also symmetric, that is the connection from node 1->2 is the same as node 2->1.
Next we plot the Directed Transfer Function which is a directed measure that is able to show when connections are not symmetrical
fig = sails.plotting.plot_vector(F.directed_transfer_function, freq_vect, diag=True)
fig.show()
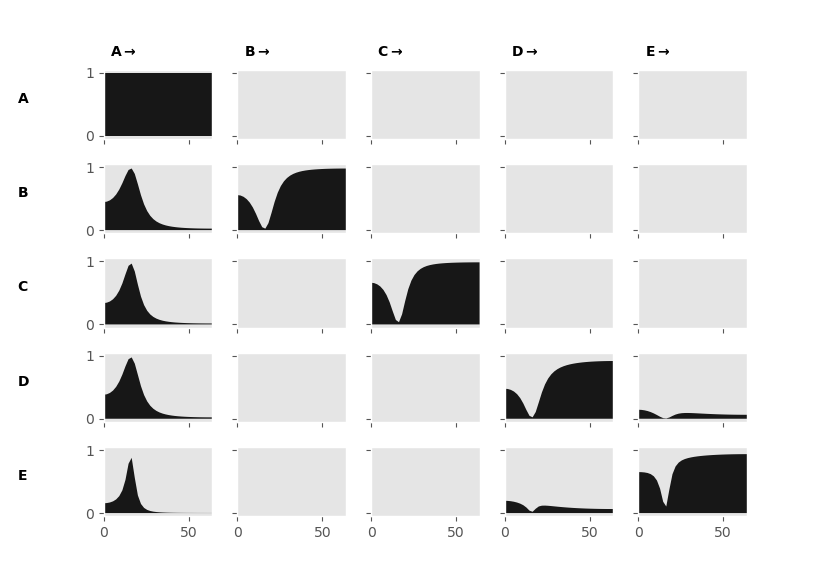
The Directed Transfer Function shows far fewer connections than the Magnitude Squared Coherence. We can now see that the connections between node 1 and the rest of the nodes are asymmetrical. This means that node 1 is driving the others. The interaction between nodes 4 and 5 is now also isolated. A remaining issue is that the Directed Transfer Function is still sensitive to indirect connections, as we can see by the power in the subplot between node 1 and 5. The Partial Directed Coherence aims to address this problem.
fig = sails.plotting.plot_vector(F.partial_directed_coherence, freq_vect, diag=True)
fig.show()
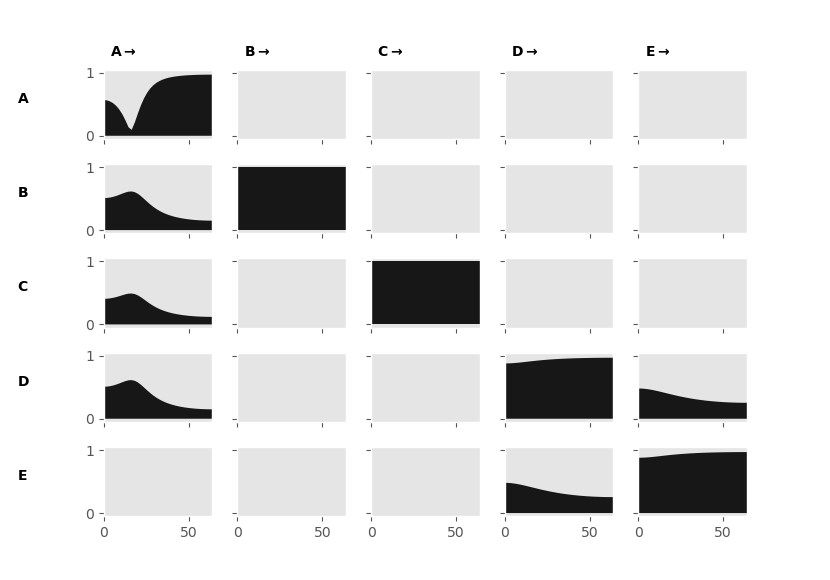
The Partial Directed Coherence now shows only the direct connections within our network. We retain our frequency resolution and the sensitivity to asymmetrical connections. There are many other MVAR derived connectivity metrics available within sails with different properties and sensitivities, these include:
Coherency (
sails.mvar_metrics.coherency(),sails.mvar_metrics.AbstractMVARMetrics.coherency)Imaginary Coherence (
sails.mvar_metrics.AbstractMVARMetrics.imaginary_coherence)Phase Coherence (
sails.mvar_metrics.AbstractMVARMetrics.phase_coherence)Magnitude Squared Coherence (
sails.mvar_metrics.AbstractMVARMetrics.magnitude_squared_coherence)Partial Coherence (
sails.mvar_metrics.partial_coherence(),sails.mvar_metrics.AbstractMVARMetrics.partial_coherence)Directed Transfer Function (
sails.mvar_metrics.directed_transfer_function(),sails.mvar_metrics.AbstractMVARMetrics.directed_transfer_function)Full Frequency Directed Transfer Function (
sails.mvar_metrics.AbstractMVARMetrics.ff_directed_transfer_function)Directed Directed Transfer Function (
sails.mvar_metrics.AbstractMVARMetrics.d_directed_transfer_function)Partial Directed Coherence (
sails.mvar_metrics.partial_directed_coherence(),sails.mvar_metrics.AbstractMVARMetrics.partial_directed_coherence)Isolated Effective Coherence (
sails.mvar_metrics.isolated_effective_coherence(),sails.mvar_metrics.AbstractMVARMetrics.isolated_effective_coherence)
In the second part of this tutorial we will look at fitting and MVAR model and the Partial Directed Coherence to simulated data, rather than from the ‘true’ model.
We can generate data from our simulated model using the
sails.simulate:AbstractSigGen.generate_signal() method and specifying the
sample_rate and number of samples to generate
X = siggen.generate_signal(sample_rate=128, num_samples=640)
X is a (nchannels x nsamples) array containing our simulated data. We can
plot X using matplotlib
import matplotlib.pyplot as plt
plt.figure()
for ii in range(5):
plt.plot(X[ii, :] + (ii * 10))
plt.show()
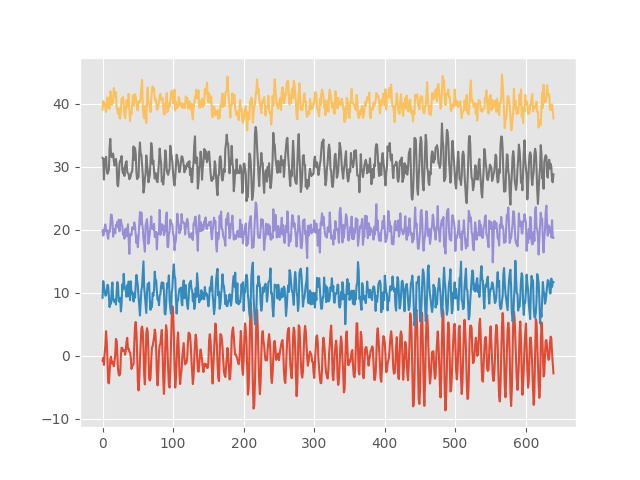
We now have a figure containing 5 time-series from our simulation. We can see there is an oscillation by eye and that some of the time-series vary together more than others.
We can fit a model to the simulated data and compute connectivity metrics as we did in previous tutorials.
delay_vect = np.arange(4)
m = sails.VieiraMorfLinearModel.fit_model(X, delay_vect)
F = sails.FourierMvarMetrics.initialise(m, sample_rate, freq_vect)
diag = m.compute_diagnostics(X)
We check that our model is fitting well by interrogating the diagnostics. Here
we see that we are explaining around 56% of the total variance in the signal
and that our model is stable (diag.SI = .91).
Let’s compare the Partial Directed Coherence from our fitted model to the Partial Directed Coherence from the ‘true’ model.
m0 = siggen.generate_model() # This is our true model
F0 = sails.FourierMvarMetrics.initialise(m0, sample_rate, freq_vect)
pdc = np.concatenate((F0.partial_directed_coherence, F.partial_directed_coherence), axis=3)
fig = sails.plotting.plot_vector(pdc, freq_vect, diag=True, line_labels=['True', 'Fitted'])
fig.show()
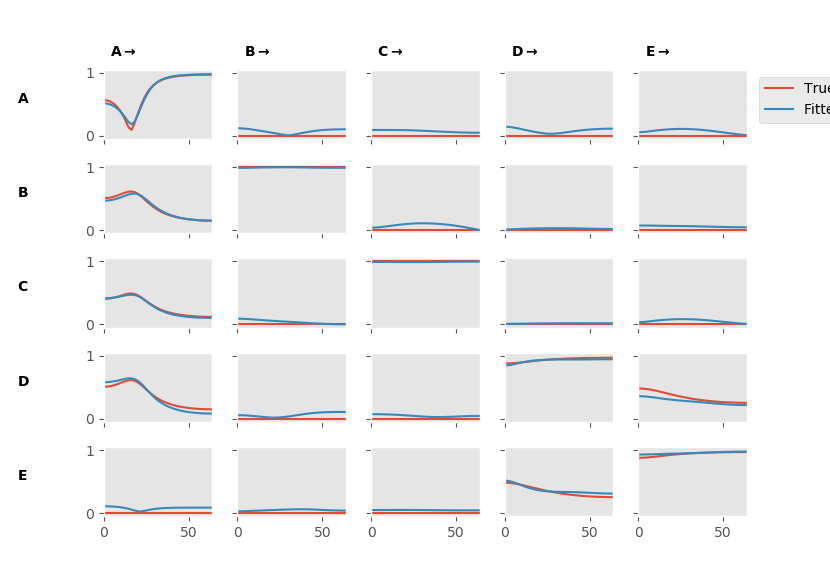
The resulting figure shows the nodes by nodes matrix of subplots containing the PDC estimates. We can see that our model is doing a pretty good job approximating the true pattern of connectivity. There may be some false-positive connections which show power for the fitted model but not for the true model.
Try re-running the simulation with a higher or lower number of samples in the
time series. You should see that the estimation starts to really break down
(lots of false positives and a distorted spectrum shape) when we have too few
samples (e.g. num_samples = 128) and becomes nearly perfect when we have a
very long time-series (e.g. num_sample = 2048)