Tutorial 8 - Using A Custom Model Fit¶
SAILS provides implementations of several algorithms for fitting autoregressive models but it is straightforward to create a custom class which implements a new model fit or uses one from another package.
This tutorial will outline how to create a custom model fit class using the
Vector Autoregression class from statsmodels.tsa. We start by importing SAILS
and creating a simulated time series to model.
import sails
# Create a simulated signal
sample_rate = 100
siggen = sails.Baccala2001_fig2()
X = siggen.generate_signal(sample_rate=sample_rate,num_samples=1000)
We then fit a model using Ordinary Least Squared as implemented in SAILS.
# Fit an autoregressive model with order 3
sails_model = sails.OLSLinearModel.fit_model(X,np.arange(4))
Now we will create a new model fit class based on
sails.modelfit.AbstractLinearModel. This is a base class which contains a
number of methods and properties to store and compute information on a model.
The AbstractLinearModel is not usable on its own as the fit_model method is
not implemented. When classes such as OLSLinearModel are defined in SAILS,
they inherit from AbstractLinearModel to define the helper functions before a
specific fit_model method is defined. We can do the same to define a custom
model fit class using an external package. We will first create a new class
which inherits from AbstractLinearModel and then define a fit_model method
which computes the model fit and stores the outputs in a standard form.
Here is our custom model fit class, each section is described in the comments in the code.
# Define a new class inheriting from the SAILS base model
class TSALinearModel( sails.AbstractLinearModel ):
# Define a fit_model method using the python @classmethod decorator
@classmethod
def fit_model( cls, data, delay_vect):
# Some sanity checking of the input matrix We make sure that the input
# data is in 2d format or 3d format with a single epoch.
# statsmodels.tsa doesn't currently support fitting multitrial data
if data.ndim == 3:
if data.shape[2] > 1:
raise ValueError('This class is only implemented for single-trial data')
# Take first trial if we have 3d data
data = data[:,:,0]
# Create object - classmethods act as object constructors. cls points
# to TSALinearModel and ret is a specific instance of TSALinearModel
# though it is currently empty.
ret = cls()
# The rest of this method will populate ret with information based on
# our model fit
# Import the model fit function
from statsmodels.tsa.api import VAR
# Initialise and fit model - we use a simple VAR with default options.
# Note that we return the model and results to ret.tsa_model. This
# means that the statsmodels.tsa.api.VAR object will be stored and
# returned with ret. Later we can use this to access the statsmodels
# model and results though the SAILS object.
ret.tsa_model = VAR(data.T) # SAILS assumes channels first, TSA samples first
model_order = len(delay_vect) - 1 # delay_vect includes a leading zero
ret.tsa_results = ret.tsa_model.fit(model_order)
# The method must assign the following values for SAILS metrics to work properly
ret.maxorder = model_order
ret.delay_vect = np.arange(model_order)
ret.parameters = np.concatenate((-np.eye(data.shape[0])[:,:,None],
ret.tsa_results.coefs.transpose((1,2,0))), axis=2)
ret.data_cov = sails.find_cov(data.T,data.T)
ret.resid_cov = sails.find_cov(ret.tsa_results.resid.T,ret.tsa_results.resid.T)
# Return fitted model within an instance of a TSALinearModel
return ret
It is crucial that the fit_model class returns an instance of our the
overall class. This instance must contain the following information. Other
functions in SAILS assume that these are stored in a fitted model class with
specific formats and names.
maxorder: the model order of the fitdelay_vect: the vector of delays used in the model fitparameters: the fitted autoregressive parameters of shape [num_channels x num_channels x model_order] with a leading identitydata_cov: the covariance matrix of the fitted dataresid_cov: the covariance matrix of the residuls of the fit
Other data can be added in as well (we store tsa_model and tsa_results
in the example here) but these five must be defined within the returned class.
We can now fit a model using our new class
tsa_model = TSALinearModel.fit_model(X,np.arange(4))
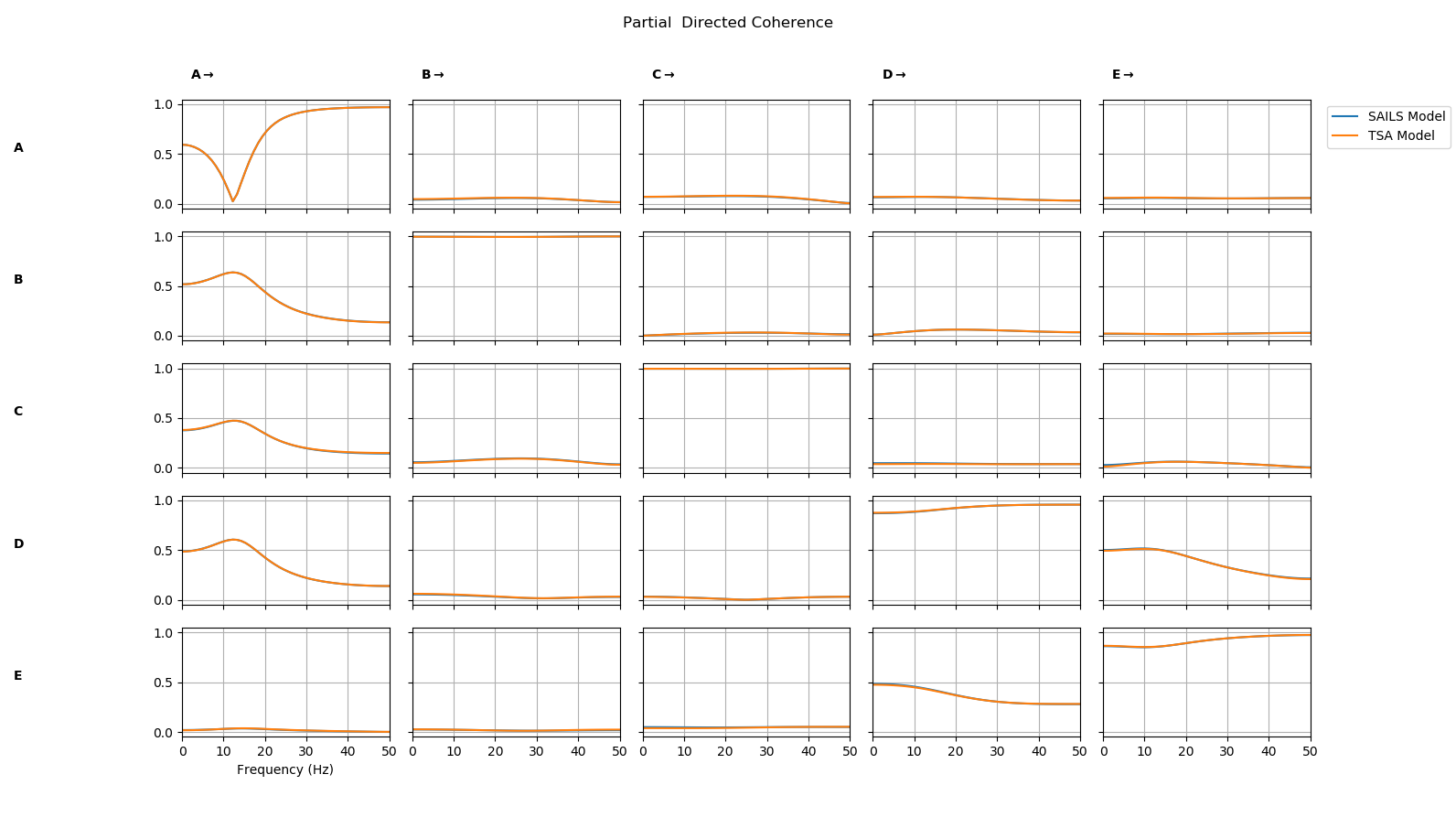
Finally, we compute connectivity metrics from each model fit and plot a comparison
freq_vect = np.linspace(0,sample_rate/2)
sails_metrics = sails.FourierMvarMetrics.initialise(sails_model,sample_rate,freq_vect)
tsa_metrics = sails.FourierMvarMetrics.initialise(tsa_model,sample_rate,freq_vect)
PDC = np.concatenate( (sails_metrics.partial_directed_coherence,tsa_metrics.partial_directed_coherence),axis=3)
sails.plotting.plot_vector(PDC,freq_vect,line_labels=['SAILS','TSA'],diag=True,x_label='Frequency (Hz'))
We see that the partial directed coherence from the two models is nearly identical.