Tutorial 1 - A pink noise system¶
In this tutorial we will demonstrate how to set up a simple univariate AR model which models a pink noise process. We will use the model to demonstrate how to extract the transfer function using both a Fourier and Modal estimator.
We start by importing the routines we will need from the numpy, sails and matplotlib. We set the ggplot style for all plots in the tutorials.
import numpy as np
from sails import generate_pink_roots, root_plot, model_from_roots
import matplotlib.pyplot as plt
plt.style.use('ggplot')
We now define the meta-parameters of our system. We will arbitrarily pretend that we are using a sampling rate of 100Hz. From this, we can compute our nyquist frequency, and a vector of frequencies at which we will evaluate measures such as our Fourier estimator. The variable freq_vect will come up often during our tutorials. In this case, we will estimate 64 frequencies which are linearly spaced between 0Hz and Nyquist. You can alter freq_vect and examine how this affects the results of the later estimations.
sample_rate = 100
nyq = sample_rate / 2.
freq_vect = np.linspace(0, nyq, 64)
As mentioned above, for our first system we will emulate a system which
behaves as a pink noise process. Whereas we would normally learn our
model from some data, for this example we will construct a model from
the polynomial form of the AR model. A function
(generate_pink_roots()) has been provided which
calculates a set of roots which will generate the appropriate roots:
roots = generate_pink_roots(1)
Given the roots of the model, we can plot these in a Z-plane representation to
examine them. A function (root_plot()) is provided to
make this straightforward.
ax = root_plot(roots)
ax.figure.show()
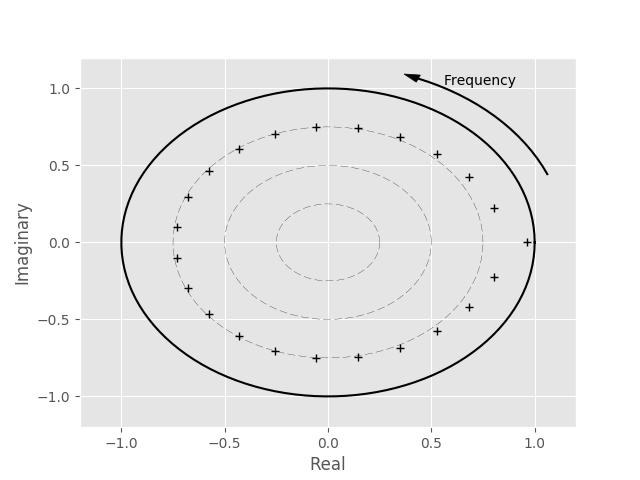
The plot shows frequency increasing counterclockwise from the x-axis. Nyquist frequency is on the negative x-axis. For real systems, the structure of the pole plot will be mirrored across the x-axis.
As mentioned above, we would normally set up a model by learning the parameters
from data. During this exploratory tutorial, we can analytically create the
model from the roots. The model_from_roots()
function will perform this task for you.
m = model_from_roots(roots)
No matter how we create our model, it will be a subclass of AbstractLinearModel.
All subclasses of AbstractLinearModel provide a number
of guarantees so that they can all be used with the various estimator routines
we discuss below. We will discuss fitting a model from data in a later
tutorial.
Now that we have our model, we can extract the transfer function (H) using two different methods. The first method extracts the transfer function using a Fourier transform of the parameters.
from sails import FourierMvarMetrics
F = FourierMvarMetrics.initialise(m, sample_rate, freq_vect)
F_H = F.H
The second method using a modal decomposition of the parameter matrix to break
the parameters apart into, hopefully, interpretable components. We first of
all create a ModalMvarMetrics and then use the
MvarModalDecomposition object inside of this to extract
the transfer function for each mode. Each mode will consist of either a pair
of poles in the complex plane or a single real mode. The
per_mode_transfer_function() will
take this into account for you.
from sails import ModalMvarMetrics
M = ModalMvarMetrics.initialise(m, sample_rate, freq_vect)
M_H = M.modes.per_mode_transfer_function(sample_rate, freq_vect)
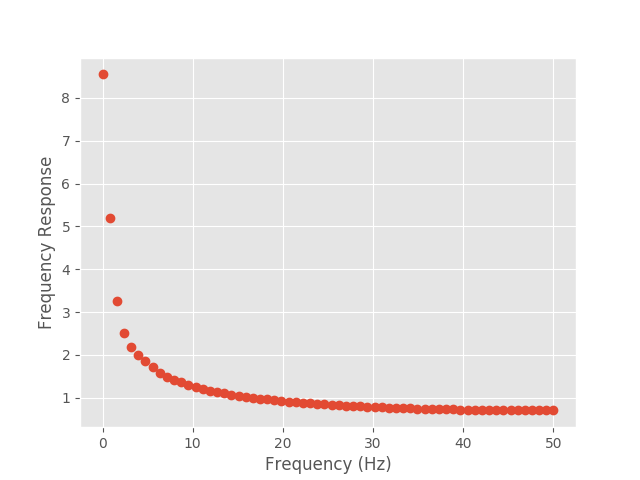
Finally, we can plot our modes in both forms to examine the relationship between them.
# Plot our fourier and modal spectra
f2 = plt.figure()
plt.plot(freq_vect, np.abs(F_H).squeeze(), 'o');
plt.plot(freq_vect, np.abs(M_H).squeeze());
plt.xlabel('Frequency (Hz)')
plt.ylabel('Frequency Response')
f2.show()